Amplitudenspektrum bestimmen

Für die Spektralanalyse der vorliegenden zeitdiskreten Signale wird die schnelle Fourier-Transformation (FFT) verwendet. Schon vor der Durchführung dieser Berechnung muss von Leakage ausgegangen werden, da es sich als fast unmöglich erweist, dass das Frequenzraster der Fourier-Transformation, genau die Frequenzen des Signals trifft, welche beobachtet werden sollen.

Um Leakage zu vermeiden kann durch eine entsprechende Fensterung der Signale eine Gewichtung stattfinden, in welcher der Effekt einer Verschmierung reduziert werden kann.

Des Weiteren muss auf Aliasing geachtet werden, ob eine Verletzung des Nyquist-Shannon-Abtasttheorems auftritt.

Die Berechnung des komplexen Amplitudenspektrums (Fourier-Transformierte) erfolgt durch
.
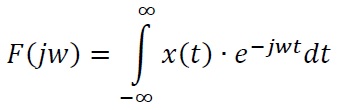Alleinige Einflussgröße stellt hier das ermittelte Spannungssignal x(t) dar.
In den unten aufgeführten Darstellungen wurde jeweils für das entsprechende Amplitudenspektrum der Betrag gebildet.

Für eine Erhöhung der spektralen Auflösung kann das sogenannte Zero-Padding verwendet werden. Großer Vorteil ist hierbei die Verwendung des FFT-Algorithmus, bei welchem die Datenmenge automatisch bis zur entsprechenden FFT Länge N mit Nullen aufgefüllt wird. Folglich erhält man eine Glättung des Amplitudenspektrums.

Im Folgenden wurde das Signal aus Versuch 3 an seiner Sprungstelle von dem negativen in den positiven Spannungsbereich untersucht. Alle auftretenden Überschwingungen außerhalb dieses Bereiches wurden mit vorgegebenen Initialisierungswerten korrigiert (aufgefüllt=padding).
Anschließend konnte mit einem erstellten Matlab-Skript das Fourier-Spektrum dargestellt werden.

Matlab-Skript:

Plot aus Matlab-Skript:

Über die beiden dargestellten Amplitudenspektren lässt sich anhand der Nyquistfrequenz bei 500 kHz die Abtastfrequenz leicht aus den Plots ablesen. In diesem Bereich machen sich auch hochfrequente Störungen bemerkbar, welche im nachfolgenden Plot genauer eingesehen werden können.

Aus den beiden Plots um die Nyqusit-Frequenz ist gut zu erkennen, dass spektrale Überlappungen auftauchen, welche man mit einer höheren Abtastrate des Oszilloskopes verhindern hätte können. Auch der zur Verfügung stehende Anti-Aliasing-Filter des Oszilloskopes konnte hier keine große Verbesserung bewirken.
Jedoch wirkt sich die Dämpfung von Störungen im hohen Frequenzbereich des digitalen Tiefpassfilters positiv auf die Darstellung des Amplitudenspektrums aus.